population genetics

Population Genetics Chpt 1 End

Chapter 1 End Problems

Problem 3

Aa X Aa produces 6 offspring, so the number of trials is 6.
Expect aa 25% of the time
and expect not aa 75% of the time.

1
2
3
4
5
6
7
8
9
probability.of.two <-(factorial(6)/(factorial(4)*factorial(2)))*(0.75^4)*(0.25^2)
probability.of.one <-(factorial(6)/(factorial(5)*factorial(1)))*(0.75^5)*(0.25^1)
probability.of.zero <-(factorial(6)/(factorial(6)))*(0.75^6)



total.probability <- probability.of.two + probability.of.one + probability.of.zero
total.probability
## [1] 0.8305664

Let’s try a brute force approach. Populate a vector of length 1000 with 250 AA, 500 Aa and 250 aa. Sample with replacement 1000 times 6 geneotype. Calculate the fraction with aa present 2 or fewer times. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
population <- c( rep("AA", 250), rep("Aa", 500), rep("aa", 250))
counts <- vector( mode='character', length=1000)

for( i in 1:1000){

     my.sample <- sample(population, 6, replace=TRUE)
     counts[i] <-  length( which(my.sample=="aa")) #each element of the vector "counts" holds the number of aa genotypes in the sample
	  
}

table(counts) #provides the counts of each genotype
## counts
##   0   1   2   3   4   5 
## 185 345 298 127  42   3
total.counts <- table(counts)[[1]] + table(counts)[[2]] + table(counts)[[3]]
total.counts  #of aa 2 or fewer times.  Divide by 1000 to get percentage
## [1] 828
## Problem 4

Jack, queen, king are the face cards so Jack is likely 1/3 of the time a face card is drawn.

There are 4 Jacks so Jack of Hearts is 1 of 4.

The probability that a randomly drawn face card (of which there are 12) is the jack of hearts is 1 of 12.

Figure out potentially relevant probabilities then answer the question.

P{FaceCard}: probability of a Face card = 12/52 = 3/13

P{Jack}: probability of a Jack = 4/52 = 1/13.

P{Hearts}: probability of a hearts = 13/52 = 1/4.

P{Jack | FaceCard}: probability of a Jack given it’s a face card = 4/12 = 1/3.

P{Jack | Hearts}: probability of a Jack given it’s a heart = 1/13.

P{Heart | Jack}: probability of a heart given a Jack = 1/4

P{FaceCard | Jack}: probability of a face card given it’s a Jack = 1

What is the probability that a randomly drawn face card is the jack of hearts?

P{JackHearts | FaceCard} = P{ Heart | Jack } X P{Jack | FaceCard}
= 1/4 x 1/3 = 1/12

Perform a trivial Bayesian analysis

Bayes Rule: P{A | B} = P{B | A}*P{A}/P{B}

What is the probability of a Jack given a face card?

There are 12 Face cards and 4 are Jacks so 4/12 or 1/3

Rewrite the Bayesian rule as: P{Jack|FaceCard} = P{FaceCard|Jack}*P{Jack}/P{FaceCard}

P{Jack|FaceCard} = (1*1/13)/3/13 = 1/3

## Problem 6 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
observed <- c( 60, 40)
#expected <- c(50, 50)  #expected with independent assortment
expected <- c(0.5, 0.5) #R expects frequencies that add to one


chisq.test( observed, p = expected, correct=FALSE )
## 
## 	Chi-squared test for given probabilities
## 
## data:  observed
## X-squared = 4, df = 1, p-value = 0.0455
chisq.test( observed, correct=FALSE ) #since equal frequencies is the default, p does not need to be specified'
## 
## 	Chi-squared test for given probabilities
## 
## data:  observed
## X-squared = 4, df = 1, p-value = 0.0455

r = 40/100 = 0.4

standard error = sqrt(( 0.4*( 1-0.4 ))/100 = 0.049

## Problem 12

This R solution requires the package “seqinr”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
template <- "tactgtgaaagatttccgact"
#the comp and many other seqinr functions require a vector of characters
#convert a string to vector of characters using s2c (sequence 2 character). c2s converts a vector back to a string.


template.complement <- comp(s2c(template))
template.complement
##  [1] "a" "t" "g" "a" "c" "a" "c" "t" "t" "t" "c" "t" "a" "a" "a" "g" "g"
## [18] "c" "t" "g" "a"
template.complement <- c2s(comp(s2c(template)))
template.complement
## [1] "atgacactttctaaaggctga"
# FRAME is 0,1, or 2

c2s(translate( s2c(template.complement), frame=0))
## [1] "MTLSKG*"
c2s(translate( s2c(template.complement), frame=1))
## [1] "*HFLKA"
#substitute an A for the first G in template

template.subs.g <- sub( "g", "a", template)
template.subs.g
## [1] "tactatgaaagatttccgact"
template.subs.g.comp <- c2s(comp(s2c(template.subs.g)))
template.subs.g.comp 
## [1] "atgatactttctaaaggctga"
c2s(translate( s2c(template.subs.g.comp), frame=0))
## [1] "MILSKG*"
template.subs.a <- sub( "c", "ca", template)
template.subs.a
## [1] "tacatgtgaaagatttccgact"
template.subs.a.comp <- c2s(comp(s2c(template.subs.a)))
template.subs.a.comp
## [1] "atgtacactttctaaaggctga"
c2s(translate( s2c(template.subs.a.comp), frame=0))
## [1] "MYTF*RL"
#When the frame is unknown, but a particular amino acid motif is desired, the "getFrame" method can be used to identify the proper frame.

getFrame <- function( pattern, seq){

  #seq must be character vector of lower case dna (not a seqFastdna object)
  #pattern is the amino acid sequence in capital letters
  #return 0,1,2 for frames 1,2,3
  #return 3 if present in more than one frame
  #return 4 if not present

  fr <- c(NA, NA, NA)

  for( i in 1:3){
    fr[i]<- words.pos(pattern, c2s(translate(  seq, frame=i-1, sens="F")))[1]
  }

  if( length( which(!is.na(fr), arr.ind=TRUE) )==1){
    result <- which(!is.na(fr), arr.ind=TRUE)-1 #subtract one because seqinar uses 0,1,2 as frames
  } else {
    if(  length( which(!is.na(fr), arr.ind=TRUE) )>1){
      result <- 3
    }else{
      result <-4}}
  return(result)
}

#The original template provides a translation with the motif "LSK"
#Translate in the frame containing this motif

c2s(translate( s2c(template.subs.a.comp), frame=getFrame("LSK",s2c(template.subs.a.comp))))
## [1] "CTLSKG*"

For a plotting example using seqinr, see

## Problem 13 
1
2
3
4
5
6
7
8
9
10
K <- 100000
N.0 <- 10000
t <- 1:100
C <- (K-N.0)/N.0
r <- 1
N <- vector("numeric", 100)

N[t] <- K/(1 + C*exp(-r*t))

plot(t, N, ylim=c(0,100000))
1
2
3
4
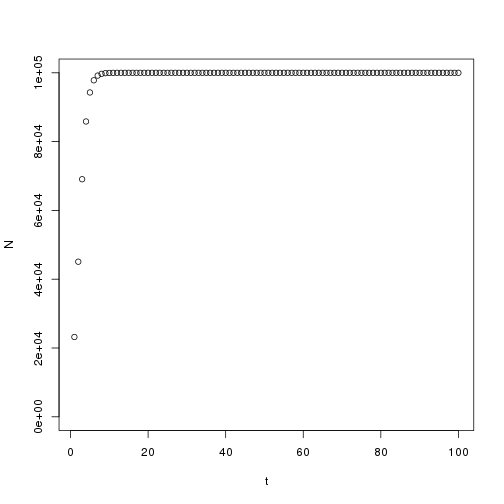
#Let's change the rate to 0.1
r <- 0.1
N[t] <- K/(1 + C*exp(-r*t))
plot(t, N, ylim=c(0,100000))
1
2
3
4
5
#It takes longer to reach the carrying capacity
#Let's change the rate to -0.1
r <- -0.1
N[t] <- K/(1 + C*exp(-r*t))
plot(t, N, ylim=c(0,100000))
1
2
3
4
5
6
7
8
9
10
#The population crashes to 0

#What if N.0 > K (rate is positive)

K <- 10000
N.0 <- 20000
r <- 1
C <- (K-N.0)/N.0
N[t] <- K/(1 + C*exp(-r*t))
plot(t, N, ylim=c(0,20000))
1
#Population drops to the carrying capacity
## Problem 14 
1
2
3
4
5
6
7
8
9
observed <- c(88, 37)
expected <- c( 0.75, 0.25)
chisq.test( observed, p = expected, correct=FALSE )
## 
## 	Chi-squared test for given probabilities
## 
## data:  observed
## X-squared = 1.4107, df = 1, p-value = 0.2349
#Accept the hypothesis of Mendelian segregation
## Problem 15 
1
2
3
4
5
6
7
8
observed <- c(269, 98, 86, 88, 30, 34, 27, 7)
expected  <-c(27/64, 9/64, 9/64, 9/64, 3/64, 3/64, 3/64, 1/64) #probabilities must sum to 1
chisq.test( observed, p = expected, correct=FALSE )
## 
## 	Chi-squared test for given probabilities
## 
## data:  observed
## X-squared = 2.673, df = 7, p-value = 0.9135
Share